
įor the following two exercises, assume that you have access to a computer program or Internet source that can generate a list of zeros and ones of any desired length. Find the first ten terms of p n p n and compare the values to π. To find an approximation for π, π, set a 0 = 2 + 1, a 0 = 2 + 1, a 1 = 2 + a 0, a 1 = 2 + a 0, and, in general, a n + 1 = 2 + a n. a1 1, an+1 2 + cos(n) n an a 1 1, a n + 1 2 + cos ( n) n a n. Therefore, being bounded is a necessary condition for a sequence to converge. Determine the convergence of the sequence defined by nNan n N a n such as.
#Prove a recursive sequence converges series#
For example, consider the following four sequences and their different behaviors as n → ∞ n → ∞ (see Figure 5.3): Using these results, we will derive a new series representation for the dilogarithm function that converges on its domain of analyticity. Since a sequence is a function defined on the positive integers, it makes sense to discuss the limit of the terms as n → ∞. Assume then that for all positive integers up to some we have. First, we show that the sequence is monotonically decreasing for all. Homework Equations The Attempt at a Solution I'm confused about the initial condition being an arbitrary positive real number. MaProve that the sequence be defined by the recursive relationship, converges and find the limit of the sequence.

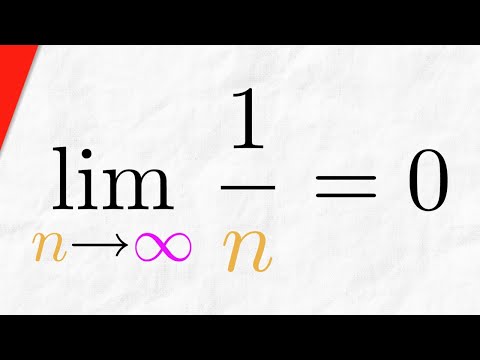
Prove that is a decreasing sequence with limit. Math Advanced Math Advanced Math questions and answers Prove that the following recursive sequence converges and find the limit: 5an A1 1 and an+1 3 + an This problem has been solved Youll get a detailed solution from a subject matter expert that helps you learn core concepts. Limit of a SequenceĪ fundamental question that arises regarding infinite sequences is the behavior of the terms as n n gets larger. 1 Mr Davis 97 1,462 44 Homework Statement Let be positive numbers. Find an explicit formula for the sequence defined recursively such that a 1 = −4 a 1 = −4 and a n = a n − 1 + 6.


 0 kommentar(er)
0 kommentar(er)
